Zeitmessung

Die Zeiteinheit «Sekunde»

Die Tageszeit ergibt sich primär aus der Rotation der Erde um ihre eigene Achse. Sie dreht sich innerhalb eines Tages um ca. 360^o (s. unten) was 15^o pro Stunde entspricht (1 Stunde = 60 Minuten = 3600 Sekunden). Seit dem Mittelalter bis 1967 war die Dauer der Zeiteinheiten (Stunde, Minute, Sekunde) an die Erdrotation gekoppelt. Im letzten Jahrhundert stellte man aber zunehmend fest, dass die Erdrotation durch äussere Einflüsse (Gezeiten, Präzession der Erdachse etc.) gestört wird, sodass die ursprüngliche Festlegung der Zeiteinheiten den heutigen Konstanz-Anforderungen nicht mehr genügte. 1967 wurde deshalb die physikalische Einheit «Sekunde» neu definiert [«Die Sekunde ist das 9 192 631 770 fache der Periodendauer der dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids ¹³³Cs entsprechenden Strahlung.»], sodass die Zeiteinheiten nicht mehr durch die Erdrotation bestimmt sind.

Sonnenzeit, Zeitzonen und Weltzeit

«Mittag, 12 Uhr Sonnenzeit» bezeichnet den Zeitpunkt des Sonnenhöchststandes, also den Moment, in dem ein senkrechter Stab im Tagesverlauf den kürzesten Schatten wirft. Diese Eigenschaft ist ortsabhängig, da der Zeitpunkt des Sonnenhöchststandes davon abhängt, auf welchem Längenkreis (Meridian) man sich befindet (zwischen Genf und St. Gallen resultiert eine Sonnenzeitdifferenz von 13 Minuten). Da derartige Lokalzeiten für unsere mobile Gesellschaft nicht praktikabel sind, hat man an der Meridian Konferenz 1884 die Welt in 24 Zeitzonen eingeteilt, die sich jeweils um ganze Stunden unterscheiden. Ausgangspunkt ist der 0^o-Meridian (Der durch die beiden Pole und die Sternwarte von Greenwich festgelegt wird). Die koordinierte Weltzeit UTC entspricht im Mittel der Sonnenzeit auf dem 0^o-Meridian und wird deshalb auch als Greenwich Mean Time (GMT) bezeichnet. Die entsprechende Zeitzone (WEZ: West-Europäische-Zeitzone) wird folglich durch die Längengrade -7.5^o und +7.5^o vorgegeben. Die Längengrade +7.5^o und +22.5^o begrenzt den Bereich der Mittel-Europäischen-Zeitzone (MEZ). Die Schweiz und viele europäische Staaten haben entschieden, dass in ihren Grenzen einheitlich die MEZ-Zeit gelten solle. Unsere Sonnenuhr befindet sich auf dem Längenkreis 7.4393^o. Zum Zentrums-Meridian MEZ (Längenkreis 15^o) ergibt sich eine Differenz von 7.5607^o. Deshalb ist der Sonnenhöchststand bei unserer Uhr 30.24 Minuten nach dem Sonnenhöchststand auf dem 15^o-Längengrad (Zentrum MEZ)

Die Zeitgleichung

Im Laufe des Jahres gibt es Differenzen zwischen der wahren Sonnenzeit (Zeitmessung: Sonnenuhr) und der mittleren Sonnenzeit (Zeitmessung: gleichmässig laufende Uhr). Die Zeitgleichung gibt die notwendige Korrektur an:

Zeitgleichung = wahre Sonnenzeit – mittlere Sonnenzeit

Es gibt zwei überlagernde Ursachen für die Differenz: a.) die elliptische Erdbahn. b.) die Neigung der Erdachse gegenüber der Ebene der Erdbahn um die Sonne.

a. Der Einfluss der elliptischen Erdbahn auf die Zeitgleichung

Johannes Kepler (1571-1630) fand als erster 1618 die korrekte Beschreibung der Planetenbahnen um die Sonne. Für die Erdbahn ausgedrückt lauten die ersten beiden (von drei) Keplerschen Gesetze:

1. Die Erde umkreist die Sonne auf einer Ellipsenbahn, wobei die Sonne in einem der beiden Brennpunkte steht.

2. In gleichen Zeiten überstreicht der Fahrstrahl zwischen Sonne und Erde dieselbe Fläche.

Aus dem zweiten Keplerschen Gesetz folgt, dass die Bahngeschwindigkeit der Erde im Perihel (kleinste Distanz Sonne-Erde = 147.09 Mio. km) am höchsten und im Aphel (grösste Distanz Sonne-Erde = 152.10 Mio. km) am kleinsten ist. Diese Variation der Bahngeschwindigkeit bringt es mit sich, dass sich die Erde im Perihel etwas mehr als im Aphel um die eigene Achse drehen muss, um von einem Sonnenhöchststand zum nächsten zu gelangen. Der Sonnentag ist im Perihel (3. Januar)  einige Sekunden länger als im Aphel (5. Juli). Diese kleinen Differenzen summieren sich auf, sodass die notwendige Korrektur Ende März -7.5 min. und Ende September +7.5 min. beträgt.

b. Der Einfluss der schräg gestellten Erdachse auf die Zeitgleichung

Auf der Seite «Zifferblatt berechnen» wird hergeleitet, dass der Sonnenhöchststand beim Erdrotationswinkel φ_o erreicht wird, wenn er aus der folgenden Gleichung berechnet wird:

φ_o = -arctan(cos ε * tan ψ )

wobei ψ für den Umlaufwinkel der Erde um die Sonne steht (Datum) und ε für den Neigungswinkel der Erdachse (ε=23.44^o) gegenüber der Ekliptik. Wenn bei einem vorgegebenen Umlaufwinkel ψ der Neigungswinkel ε gleich Null wäre, würde gemäss der obigen Formel φ_o = ψ. So lange die Erdachse senkrecht auf der Ekliptik steht, sind keine Korrekturen Δφ angebracht. Setzt man nun den realen Wert für ε ein, so resultiert eine Korrektur:

Δφ = ψ – arctan(cos ε * tan ψ )

Bei ψ = 0^o (Frühlingspunkt) und ψ = 180^o (Herbstpunkt) wird die Korrektur Δφ = 0. Bei ψ = 90^o und ψ = 270^o hat der Tangens Singularitäten. Eine Grenzwertrechnung zeigt aber, dass auch in diesen Punkten die Korrektur Δφ gleich Null wird. Maximale Korrekturen ergeben sich bei ψ = 45^o und ψ = 225^o mit Δφ = 2.5^o respektive bei ψ = 135^o und ψ = 315^o mit Δφ = -2.5^o.

Die Rotationsgeschwindigkeit der Erde beträgt annähernd 360^o/(24 h * 60 min/h) = 0.25^o/min. Die maximalen zeitlichen Korrekturen für die geneigte Erdachse betragen folglich ±10 min.

Die beiden Korrekturen [a. und b.] werden in der Zeitgleichung aufsummiert, wobei die Amplituden aber nicht synchronisiert sind, was zur asymmetrischen Form der Kurve führt.

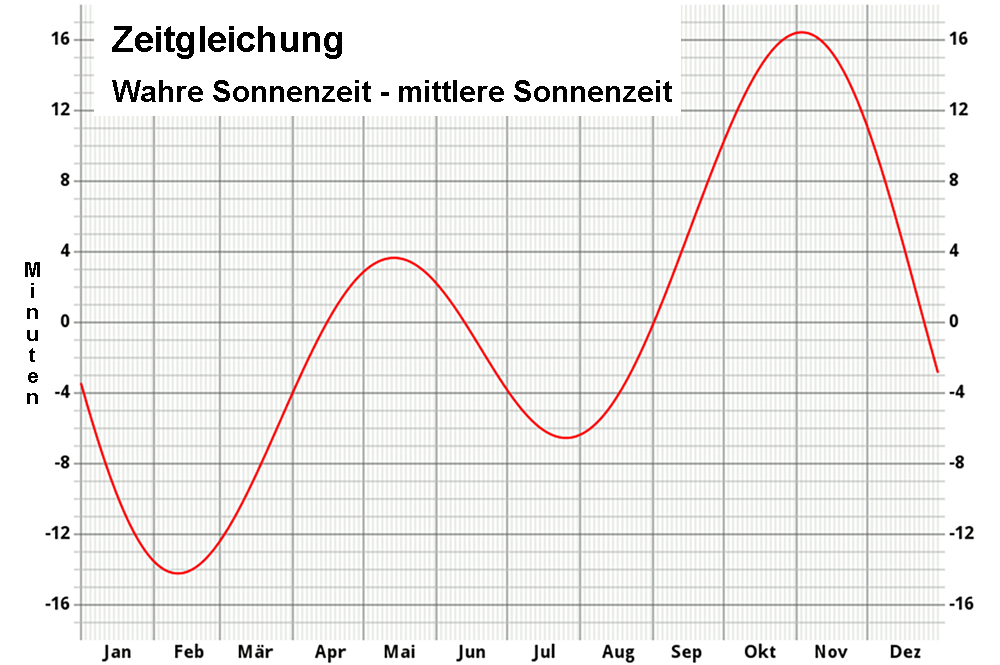
Die Zeitgleichung kann man ebenso, wie andere Korrekturen in der Zeit-Skala berücksichtigen, damit die Sonnenuhr die Weltzeit anzeigt.